Floor And Ceiling Function In Discrete Maths

This set of discrete mathematics multiple choice questions answers mcqs focuses on floor and ceiling function.

Floor and ceiling function in discrete maths.

Int limits 0 infty lfloor x rfloor e x dx. Cs 2336 discrete mathematics author. Let a and b be real numbers with a b. 0 x.

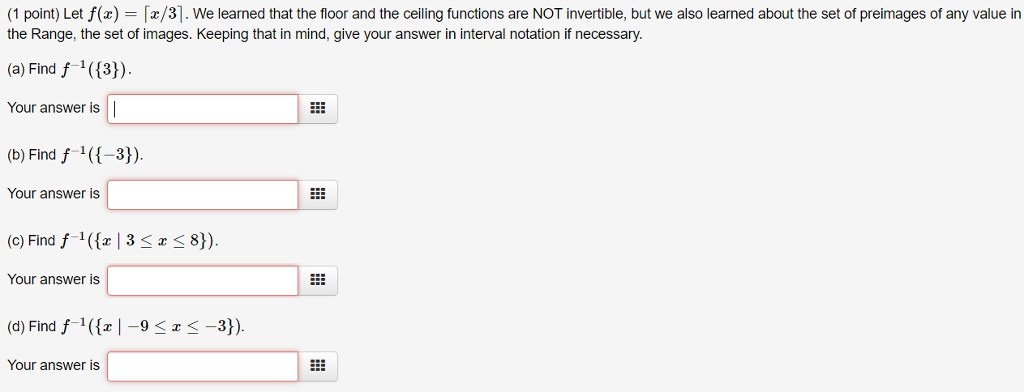
Please briefly explain that the function you propose is one to one and onto. And this is the ceiling function. The int function short for integer is like the floor function but some calculators and computer programs show different results when given negative numbers. One is the floor function and the other is the ceiling function for example the floor and ceiling of a decimal 3 31 are 3 and 4 respectively.

In mathematics and computer science the floor function is the function that takes as input a real number and gives as output the greatest integer less than or equal to denoted or similarly the ceiling function maps to the least integer greater than or equal to denoted or. The best strategy is to break up the interval of integration or summation into pieces on which the floor function is constant. For example and while. If this set is countable prove it by proposing a bijection a oneto one and onto function between this set and the set of positive integers z.

In mathematics and computer programming two important functions are used quite often. Browse other questions tagged functions discrete mathematics inequality or ask your own question. Evaluate 0 x e x d x. Since we know that x n if and only if x n n integer.

A floor function map a real number to a smallest previous integer b greatest previous integer c smallest following integer d none of the mentioned view answer. Floor and ceiling functions let x be a real number the floor function of x denoted by x is the largest integer that is smaller than or equal to x the ceiling function of x denoted by x is the. Definite integrals and sums involving the floor function are quite common in problems and applications.